Mastering Karnaugh Maps: A Complete Information to 4-Variable Minimization

Associated Articles: Mastering Karnaugh Maps: A Complete Information to 4-Variable Minimization

Introduction

With enthusiasm, let’s navigate by the intriguing matter associated to Mastering Karnaugh Maps: A Complete Information to 4-Variable Minimization. Let’s weave fascinating data and provide recent views to the readers.

Mastering Karnaugh Maps: A Complete Information to 4-Variable Minimization

Karnaugh maps (Ok-maps) are invaluable instruments in digital logic design, providing a visible and intuitive technique for simplifying Boolean expressions. Whereas relevant to numerous numbers of variables, their effectiveness is especially pronounced with 4 variables, the place conventional algebraic manipulation can develop into cumbersome and error-prone. This text gives a complete exploration of Ok-maps for 4 variables, overlaying their development, simplification methods, and sensible functions.

Understanding the Basis: Boolean Algebra and Minimization

Earlier than delving into Ok-maps, it is essential to know the underlying ideas of Boolean algebra and the significance of minimization. Boolean algebra offers with binary variables (0 and 1, representing false and true) and logical operations like AND, OR, and NOT. A Boolean expression describes a logical operate, mapping inputs to an output. Minimizing a Boolean expression means discovering an equal expression with the fewest phrases and literals (variables and their enhances). Minimization results in easier, extra environment friendly, and cost-effective digital circuits. It reduces the variety of logic gates required, reducing energy consumption and enhancing circuit pace.

Setting up a 4-Variable Karnaugh Map

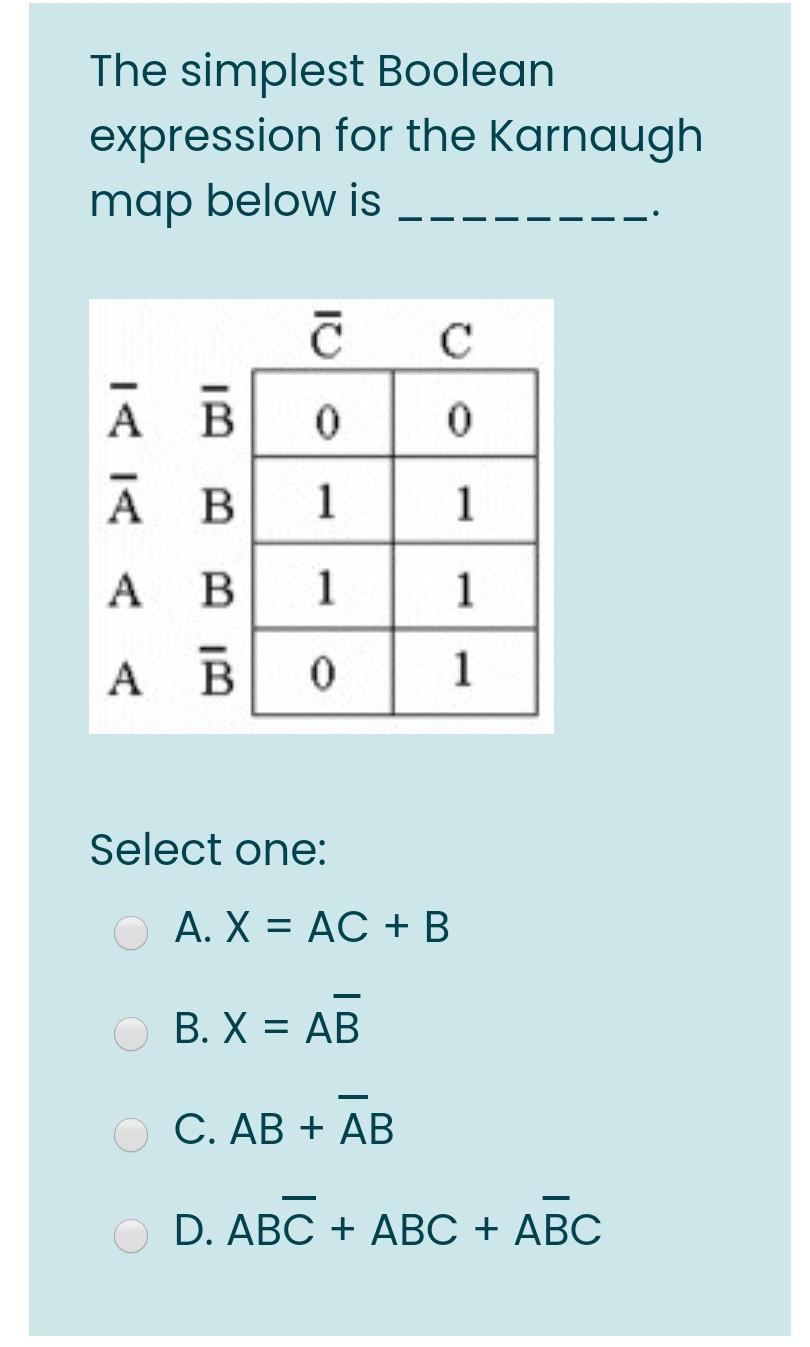
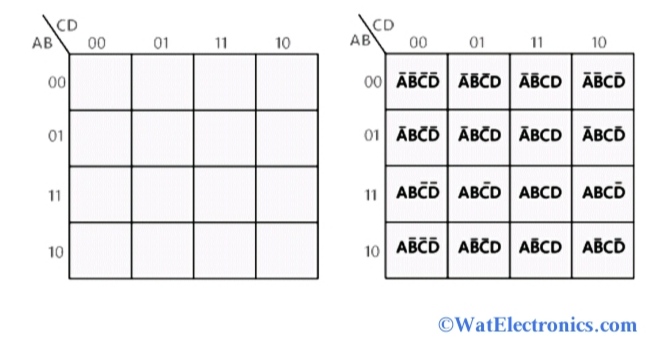
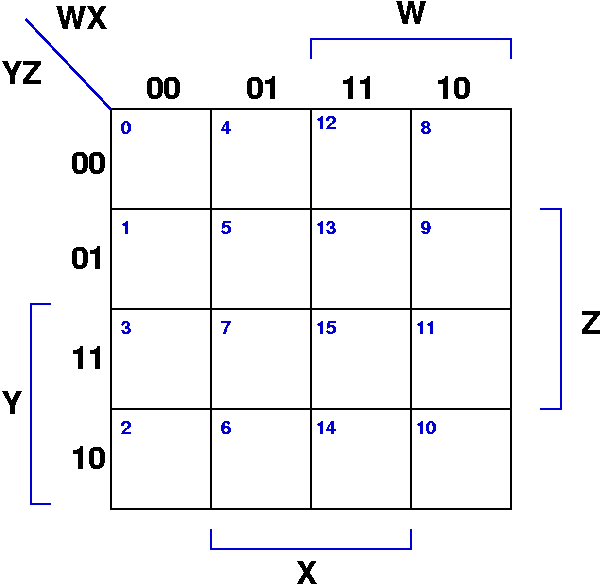
A four-variable Ok-map is a two-dimensional illustration of a fact desk, organized to facilitate the identification of adjoining minterms (or maxterms) that may be mixed for simplification. It consists of a 4×4 grid, the place every cell corresponds to a singular minterm (a product time period representing a particular mixture of enter values). The association of the cells is essential: adjoining cells differ by just one variable. This adjacency is essential to the simplification course of.

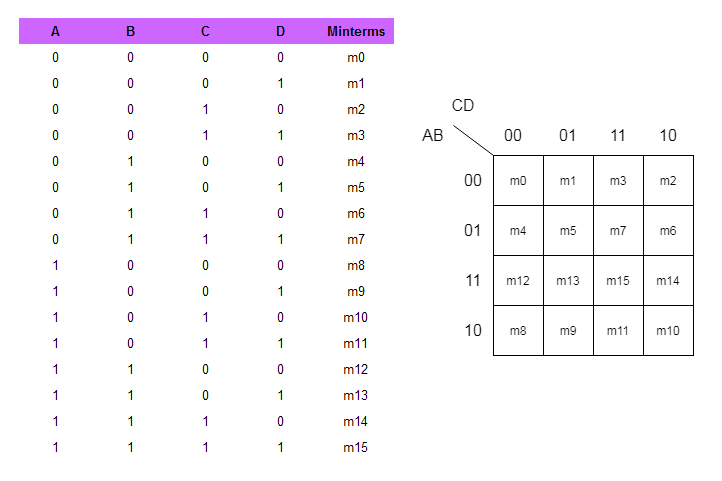
The variables are usually labeled alongside the highest and facet of the map. A standard conference is to make use of ABCD, the place A is essentially the most vital bit (MSB) and D is the least vital bit (LSB). The rows and columns are organized in Grey code order, not binary order. Grey code ensures that adjoining cells differ by just one bit, a crucial property for Ok-map simplification. A typical four-variable Ok-map seems to be like this:

     CD
AB  00  01  11  10
00  m0  m1  m3  m2
01  m4  m5  m7  m6
11  m12 m13 m15 m14
10  m8  m9  m11 m10

The place m0, m1, m2, and so on., characterize the minterms akin to the enter combos. For instance, m0 represents the minterm the place A=0, B=0, C=0, and D=0.

Getting into Information into the Ok-Map

As soon as the Ok-map is constructed, the following step is to populate it with the output values (0 or 1) from the reality desk. Every cell corresponds to a particular mixture of inputs and its corresponding output. As an example, if the output for the enter mixture A=0, B=0, C=0, D=0 is 1, then a ‘1’ is positioned within the top-left cell (m0). If the output is 0, a ‘0’ is positioned.

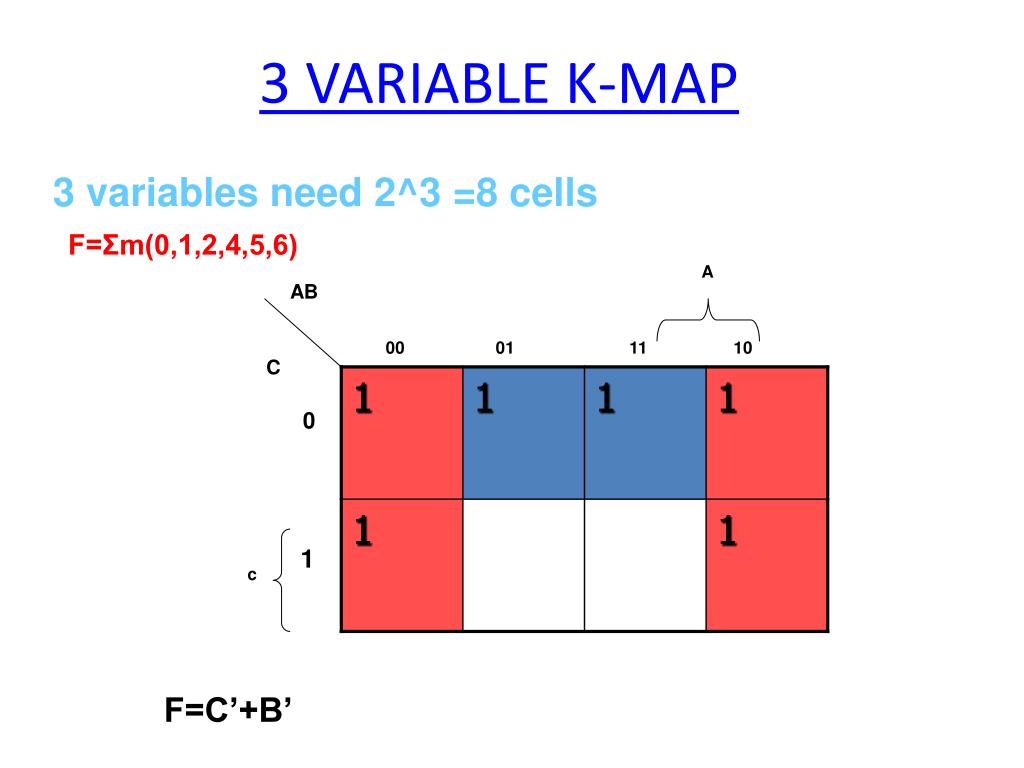
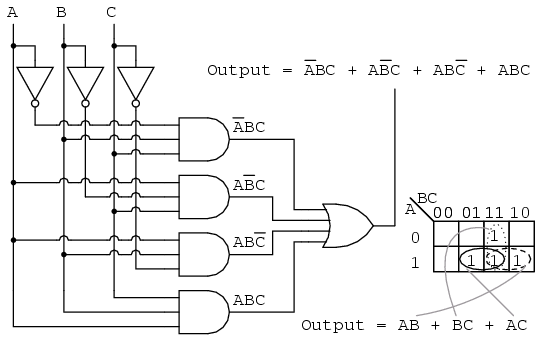
Simplifying Boolean Expressions utilizing Ok-Maps: Grouping Strategies

The ability of Ok-maps lies of their capability to visually simplify Boolean expressions. The simplification course of entails grouping adjoining cells containing ‘1’s. These teams have to be rectangular and include an influence of two (1, 2, 4, 8, and so on.) variety of cells. Bigger teams result in easier expressions.

Listed here are the important thing ideas for grouping:

• Adjoining Cells: Cells sharing a standard edge are thought of adjoining. Notice the wrap-around impact: the leftmost column is adjoining to the rightmost column, and the topmost row is adjoining to the bottommost row.
• Group Dimension: Teams needs to be as giant as potential, adhering to the power-of-2 rule.
• Overlap: Teams can overlap. A single cell can belong to a number of teams.
• Minimal Teams: Intention for the fewest variety of teams to cowl all ‘1’s.

Examples of 4-Variable Ok-Map Simplification

Let’s illustrate the simplification course of with just a few examples:

Instance 1:

Suppose a four-variable Ok-map has ‘1’s in cells m0, m1, m2, m3, m8, m9, m10, m11. These cells kind two teams of 4: one overlaying the highest row and one other overlaying the underside row. This simplifies to A' + B.

Instance 2:

Take into account a Ok-map with ‘1’s in cells m0, m1, m4, m5, m10, m11, m14, m15. These cells may be grouped into two teams of eight, resulting in a simplified expression of A'D' + AD.

Instance 3 (Illustrating Overlapping Teams):

Think about a Ok-map with ‘1’s in cells m0, m1, m3, m4, m5, m7. These may be grouped in a number of methods. One optimum grouping would contain a bunch of 4 (m0, m1, m4, m5) and a bunch of two (m3, m7). This ends in a simplified expression that’s extra environment friendly than grouping them in another way.

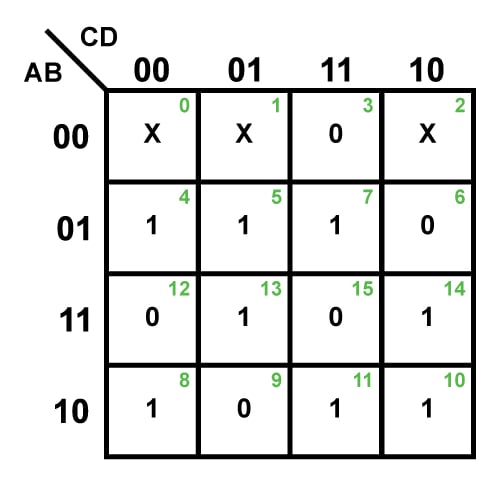
Coping with Do not Care Circumstances

Generally, sure enter combos are irrelevant or "do not care" situations. These are denoted by ‘X’ within the Ok-map. Do not care situations may be strategically used to enlarge teams, resulting in additional simplification. They are often handled as both 0 or 1, whichever results in a bigger group and an easier expression.

Prime Implicants and Important Prime Implicants

In additional advanced Ok-maps, the idea of prime implicants turns into essential. A major implicant is a bunch of ‘1’s that can’t be additional mixed with different ‘1’s to kind a bigger group. An important prime implicant is a primary implicant that covers no less than one ‘1’ that isn’t coated by some other prime implicant. Figuring out important prime implicants is essential for acquiring a minimal sum-of-products (SOP) expression.

Limitations and Options to Ok-Maps

Whereas Ok-maps are efficient for as much as 4 variables, their complexity will increase quickly with extra variables. For 5 or extra variables, different minimization methods such because the Quine-McCluskey algorithm or specialised software program instruments are sometimes most popular. These algorithms present a scientific method to Boolean minimization, particularly for bigger and extra advanced features.

Purposes of 4-Variable Ok-Maps

4-variable Ok-maps discover widespread utility in varied points of digital logic design, together with:

• Simplifying combinational logic circuits: Ok-maps are used to design environment friendly circuits for features like adders, multiplexers, decoders, and encoders.
• Designing sequential circuits: State minimization in finite state machines (FSMs) can leverage Ok-maps for simplifying state transition tables.
• Simplifying Boolean expressions in programming: Ok-maps can be utilized to optimize Boolean expressions inside programming logic, notably in embedded methods programming.

Conclusion

Karnaugh maps present a strong and intuitive technique for minimizing four-variable Boolean expressions. By understanding the ideas of Ok-map development, grouping methods, and the dealing with of do not care situations, designers can create environment friendly and optimized digital circuits. Whereas limitations exist for higher-variable features, Ok-maps stay a vital software within the digital logic designer’s arsenal, providing a visible and simple method to Boolean simplification that enhances understanding and effectivity in circuit design. Mastering Ok-maps is a foundational talent for anybody working with digital logic methods.

Closure

Thus, we hope this text has supplied helpful insights into Mastering Karnaugh Maps: A Complete Information to 4-Variable Minimization. We admire your consideration to our article. See you in our subsequent article!